CNN 基础知识,本文转载一下,是之前入门的时候看的,一些概念解释的比较清楚,并且配合动图,应该一看就懂。主要包括卷积介绍,以及填充、步长等的计算。
- 原文地址:https://zhuanlan.zhihu.com/p/77471866
卷积神经网络(convolutional neural network,CNN)是指至少在网络的一层中使用卷积运算来代替一般的矩阵乘法运算的神经网络,因此命名为卷积神经网络。那什么是卷积运算啊?接下来我们一起来揭开它神秘的面纱。
卷积 (Convolution)
我们以灰度图像为例进行讲解:从一个小小的权重矩阵,也就是卷积核(kernel)开始,让它逐步在二维输入数据上“扫描”。卷积核“滑动”的同时,计算权重矩阵和扫描所得的数据矩阵的乘积,然后把结果汇总成一个输出像素。
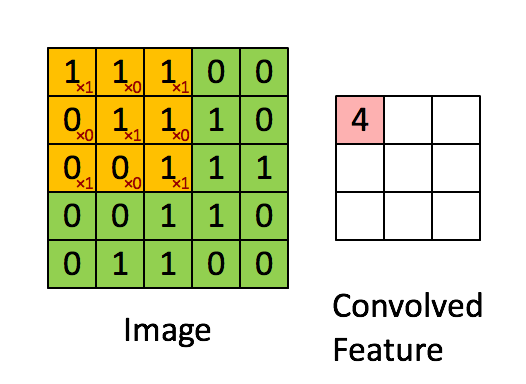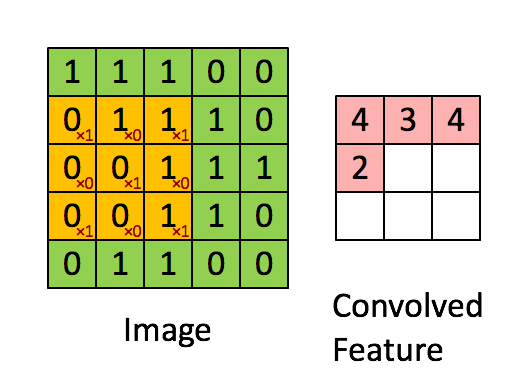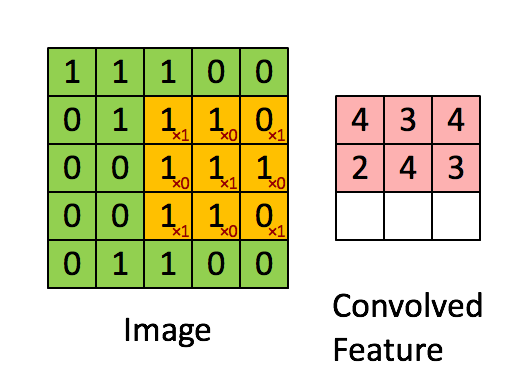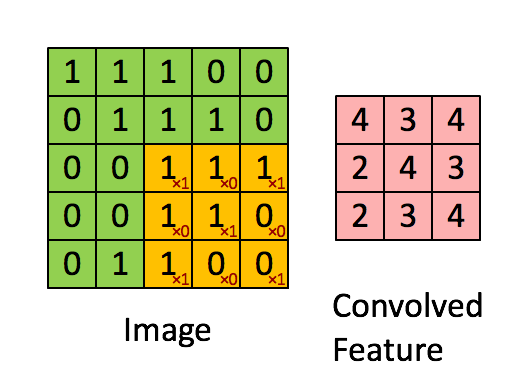
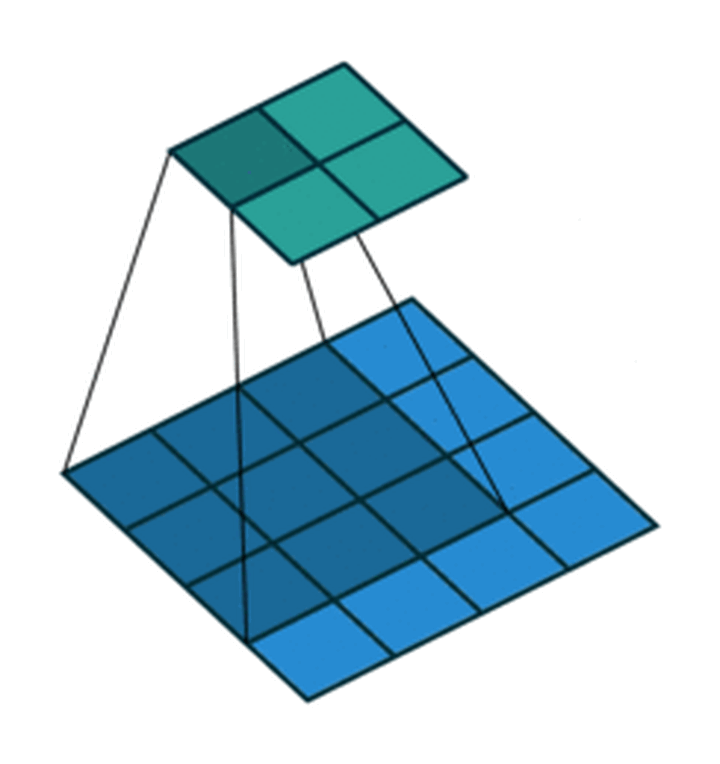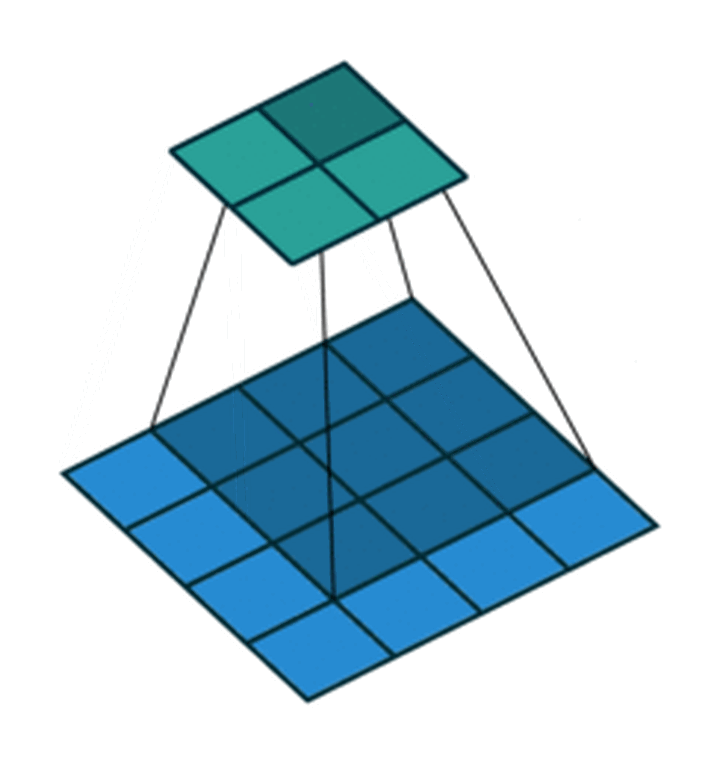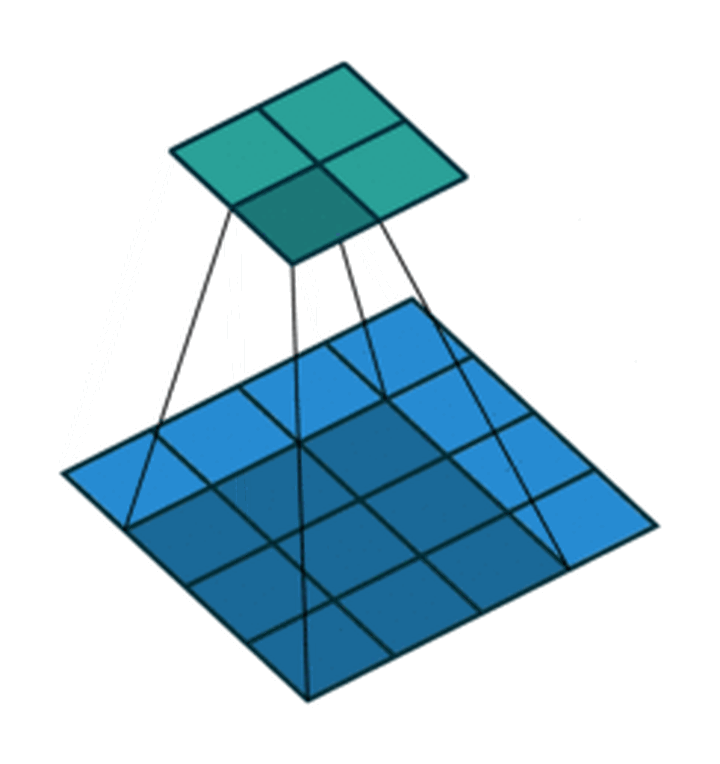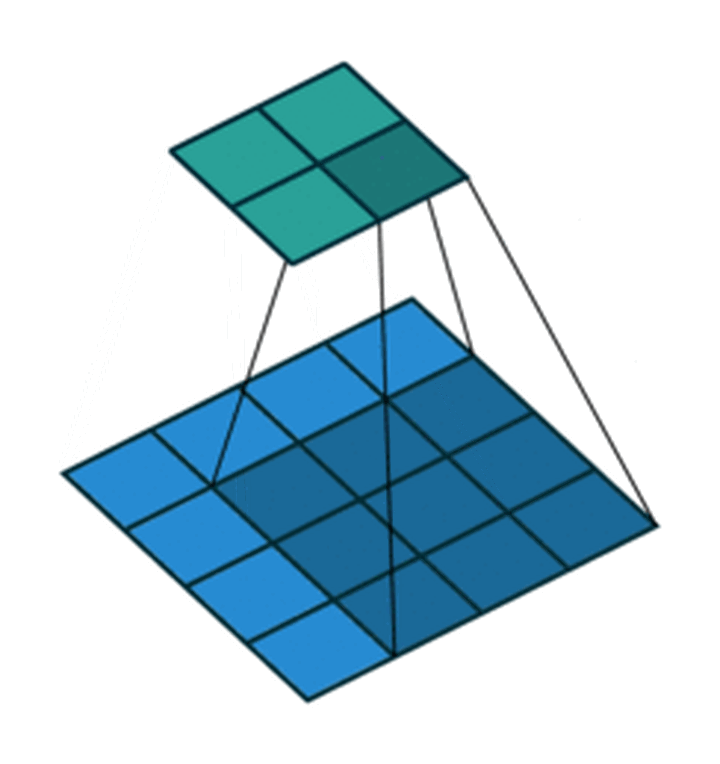
深度学习里面所谓的卷积运算,其实它被称为互相关(cross-correlation)运算:将图像矩阵中,从左到右,由上到下,取与滤波器同等大小的一部分,每一部分中的值与滤波器中的值对应相乘后求和,最后的结果组成一个矩阵,其中没有对核进行翻转。
填充 (Padding)
前面可以发现,输入图像与卷积核进行卷积后的结果中损失了部分值,输入图像的边缘被“修剪”掉了(边缘处只检测了部分像素点,丢失了图片边界处的众多信息)。这是因为边缘上的像素永远不会位于卷积核中心,而卷积核也没法扩展到边缘区域以外。
这个结果我们是不能接受的,有时我们还希望输入和输出的大小应该保持一致。为解决这个问题,可以在进行卷积操作前,对原矩阵进行边界填充(Padding),也就是在矩阵的边界上填充一些值,以增加矩阵的大小,通常都用“0”来进行填充的。
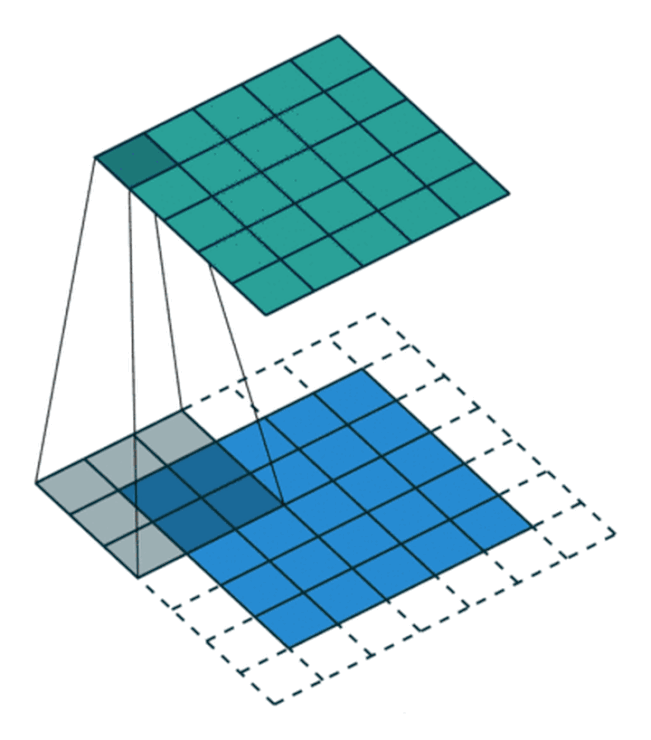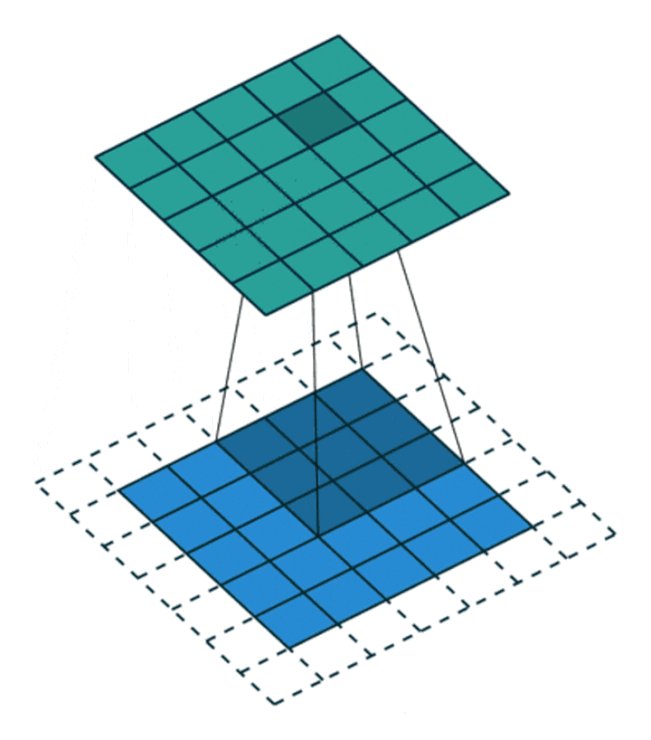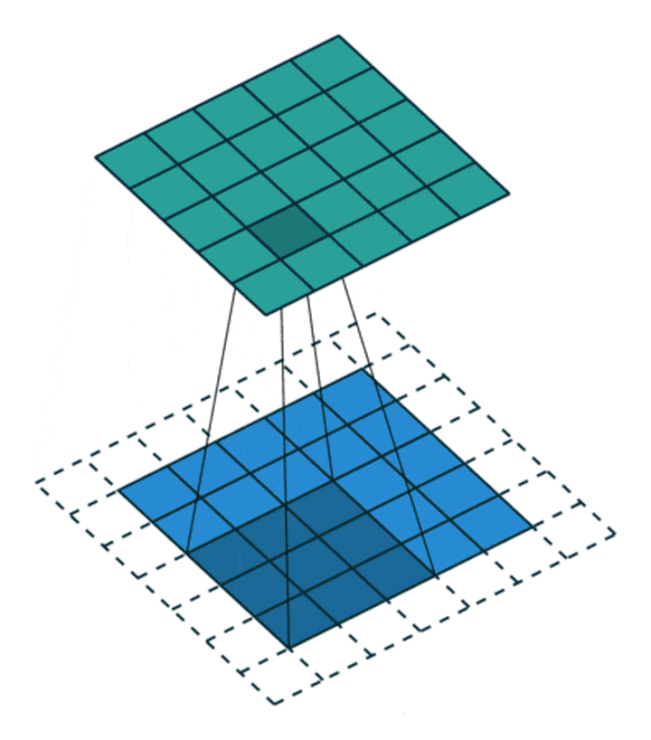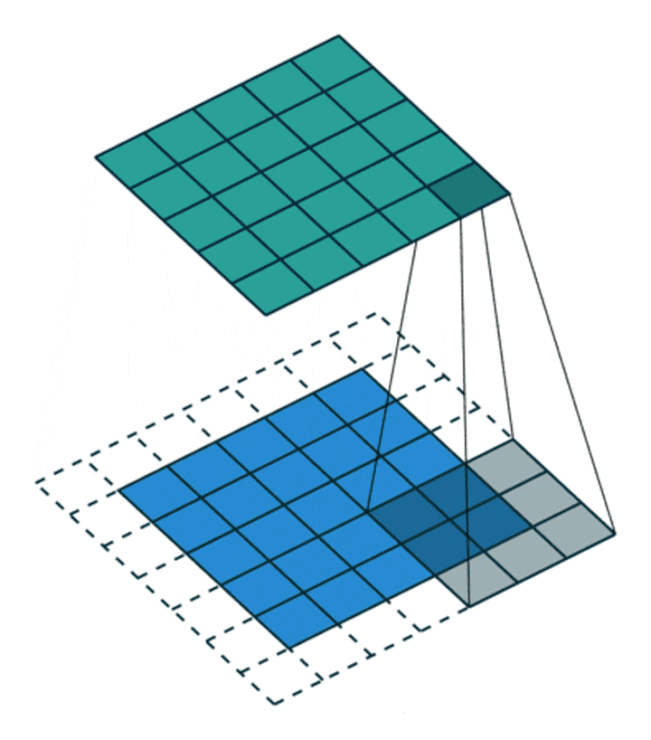
通过填充的方法,当卷积核扫描输入数据时,它能延伸到边缘以外的伪像素,从而使输出和输入size相同。
常用的两种padding:
(1)valid padding:不进行任何处理,只使用原始图像,不允许卷积核超出原始图像边界
(2)same padding:进行填充,允许卷积核超出原始图像边界,并使得卷积后结果的大小与原来的一致
步长 (Stride)
滑动卷积核时,我们会先从输入的左上角开始,每次往左滑动一列或者往下滑动一行逐一计算输出,我们将每次滑动的行数和列数称为Stride,在之前的图片中,Stride=1;在下图中,Stride=2。
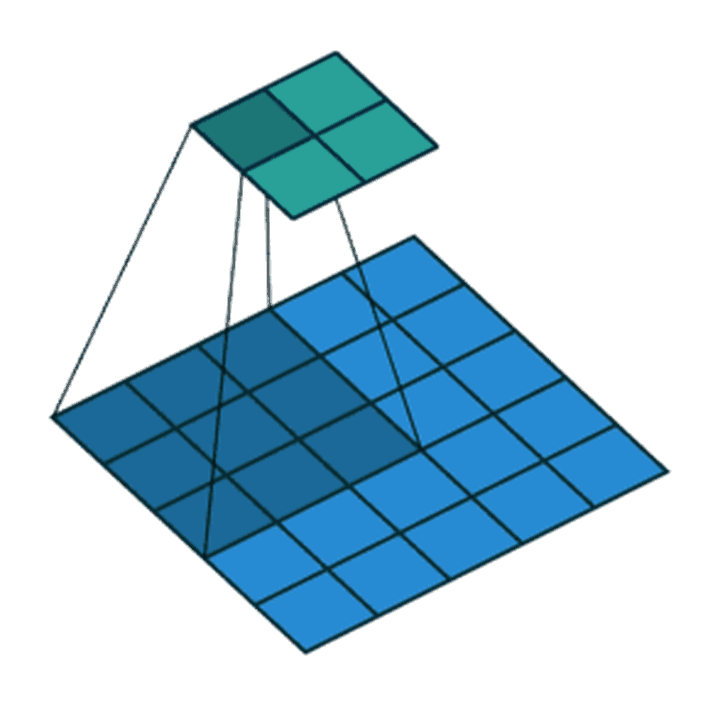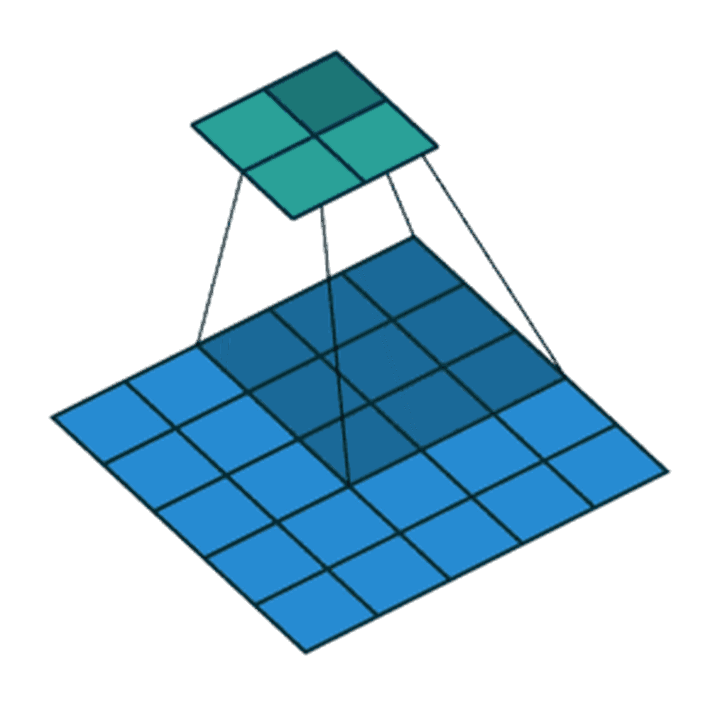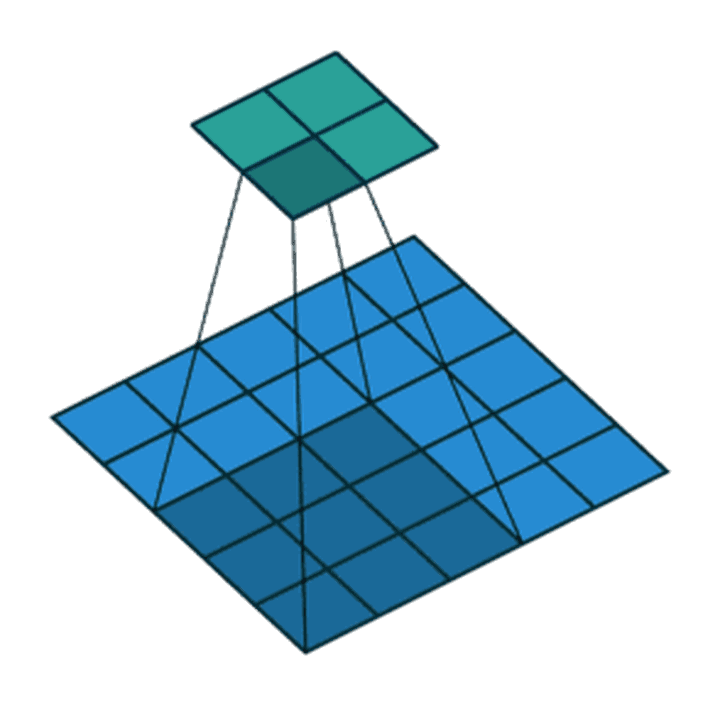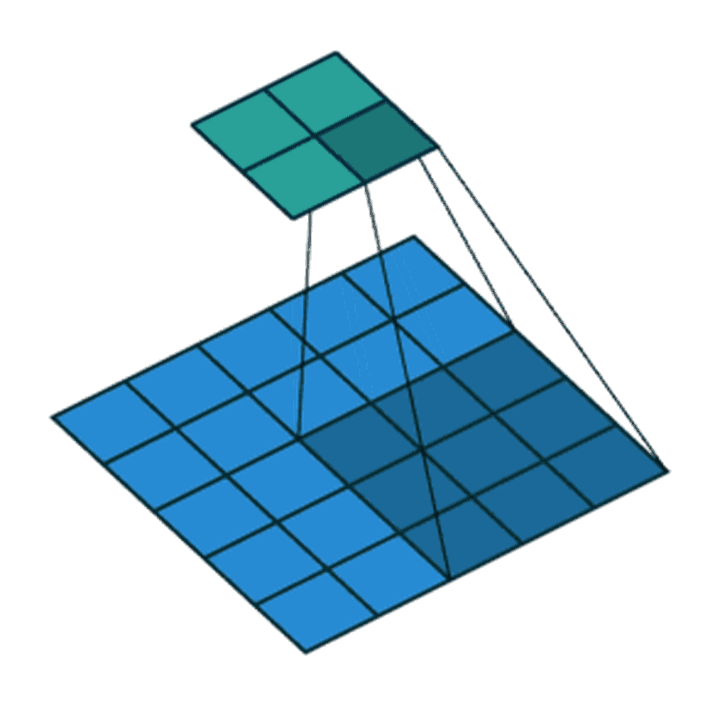
卷积过程中,有时需要通过padding来避免信息损失,有时也要在卷积时通过设置的步长(Stride)来压缩一部分信息,或者使输出的尺寸小于输入的尺寸。
Stride的作用:是成倍缩小尺寸,而这个参数的值就是缩小的具体倍数,比如步幅为2,输出就是输入的1/2;步幅为3,输出就是输入的1/3。以此类推。
【卷积核的大小一般为奇数*奇数】 1*1,3*3,5*5,7*7都是最常见的。这是为什么呢?为什么没有偶数*偶数?
(1)更容易padding
在卷积时,我们有时候需要卷积前后的尺寸不变。这时候我们就需要用到padding。假设图像的大小,也就是被卷积对象的大小为n*n,卷积核大小为k*k,padding的幅度设为(k-1)/2时,卷积后的输出就为(n-k+2*((k-1)/2))/1+1=n,即卷积输出为n*n,保证了卷积前后尺寸不变。但是如果k是偶数的话,(k-1)/2就不是整数了。
(2)更容易找到卷积锚点
在CNN中,进行卷积操作时一般会以卷积核模块的一个位置为基准进行滑动,这个基准通常就是卷积核模块的中心。若卷积核为奇数,卷积锚点很好找,自然就是卷积模块中心,但如果卷积核是偶数,这时候就没有办法确定了,让谁是锚点似乎都不怎么好。
卷积的计算公式

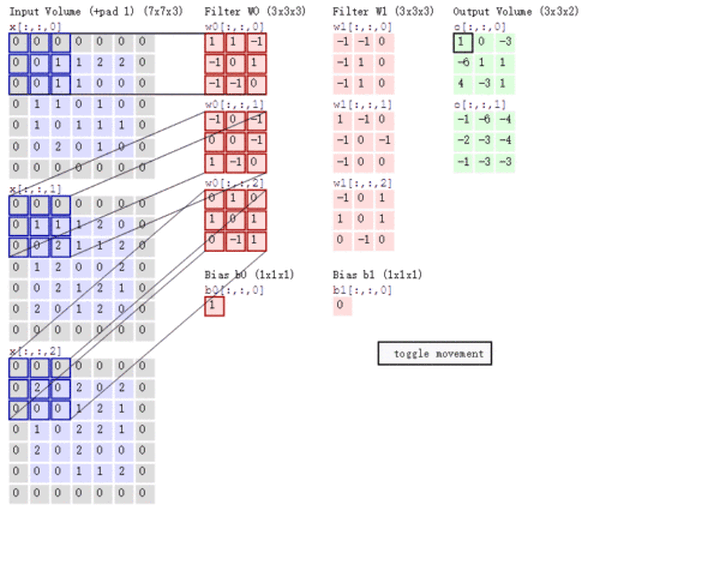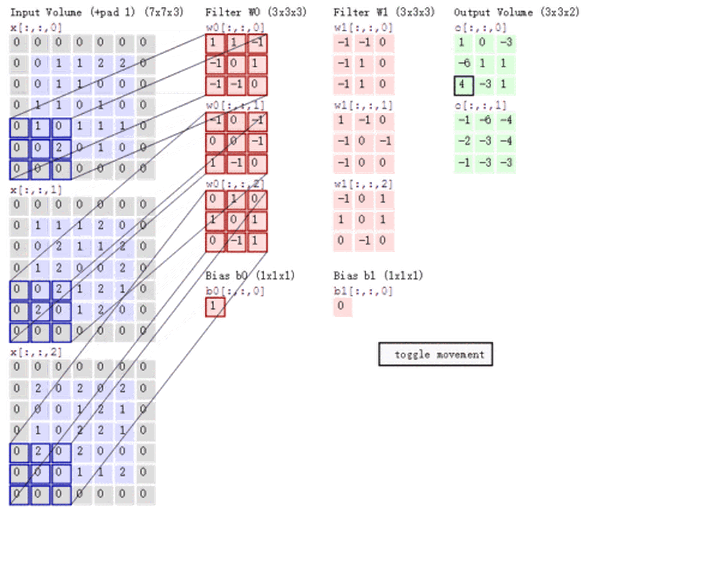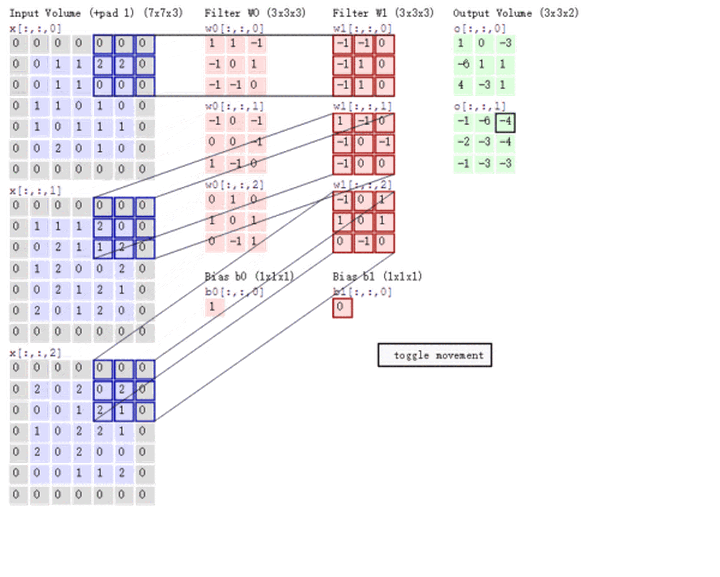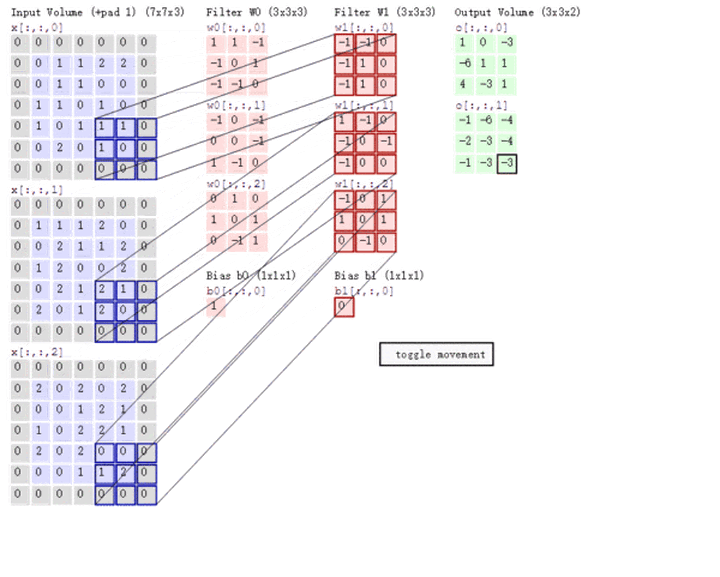
多通道卷积
上述例子都只包含一个输入通道。实际上,大多数输入图像都有 RGB 3个通道。
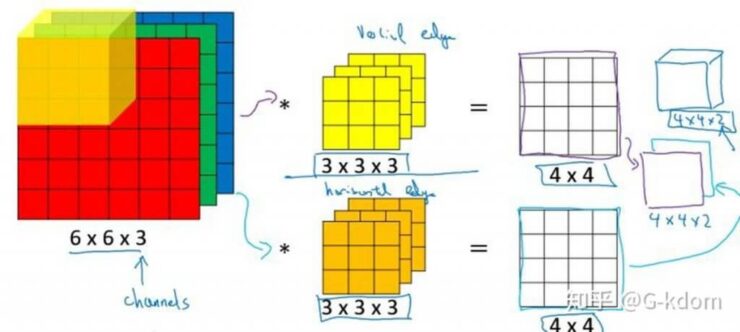
这里就要涉及到“卷积核”和“filter”这两个术语的区别。在只有一个通道的情况下,“卷积核”就相当于“filter”,这两个概念是可以互换的。但在一般情况下,它们是两个完全不同的概念。每个“filter”实际上恰好是“卷积核”的一个集合,在当前层,每个通道都对应一个卷积核,且这个卷积核是独一无二的。
多通道卷积的计算过程:将矩阵与滤波器对应的每一个通道进行卷积运算,最后相加,形成一个单通道输出,加上偏置项后,我们得到了一个最终的单通道输出。如果存在多个filter,这时我们可以把这些最终的单通道输出组合成一个总输出。
这里我们还需要注意一些问题——滤波器的通道数、输出特征图的通道数。
某一层滤波器的通道数 = 上一层特征图的通道数。如上图所示,我们输入一张 6×6×3 的RGB图片,那么滤波器( 3×3×3 )也要有三个通道。
某一层输出特征图的通道数 = 当前层滤波器的个数。如上图所示,当只有一个filter时,输出特征图( 4×4 )的通道数为1;当有2个filter时,输出特征图(4×4×2 )的通道数为2。